Question

Use I'Hopital's Rule more than once to rewrite the limit in its final form as lim x --> 0

lim x --> 0 e^x -sinx - 1/ x^4 + 7x^3 + 8x^2

Answer 1

To compute the limit

`\displaystyle\lim_(x\to0)(e^x-\sin x-1)/(x^4+7x^3+8x^2)`

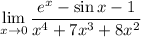
notice that when x = 0, both the numerator and denominator converge to 0. Apply l'Hopital's rule once gives

`\displaystyle\lim_(x\to0)(e^x-\cos x)/(4x^3+21x^2+16x)`

but again, this returns the indeterminate form 0/0. Applying again gives

`\displaystyle\lim_(x\to0)(e^x+\sin x)/(12x^2+42x+16)`

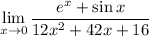
so that the numerator converges to e⁰ + sin(0) = 1, and the denominator converges to 12•0² + 42•0 + 16 = 16.

So the limit is 1/16.