Question

A plane is to be loaded with bottles of water and medical supplies to be sent to victims of an earthquake. Each bottle of water serves 10 people and each medical kit aids six people. The goal is to maximize z, the total number of people helped, where z = 10x + 6y, and x is the number of bottles and y is the number of medical kits. Using the constraints of the situation (plane weight and volume capacities) the shaded region is in the graph is obtained. Which vertex of the region represents the solution to the maximization problem?

Answer 1

C) (2000, 4000)

Explanation:

Answer 2

The vertex that maximize the problem is (2,000,4,000)

Explanation:

we have

`z=10x+6y`

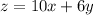
The vertex of the shaded region are

A(0,0), B(4,000,0),C(2,000,4,000), D(0,6,000)

Substitute the value of x and the value of y of each vertex in the z equation to find the solution

case A) A(0,0)

`z=10(0)+6(0)=0`

case B) B(4,000,0)

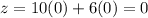
`z=10(4,000)+6(0)=40,000`

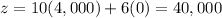
case C) C(2,000,4,000)

`z=10(2,000)+6(4,000)=44,000`

case D) D(0,6,000)

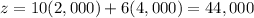
`z=10(0)+6(6,000)=36,000`

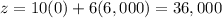
therefore

The vertex that maximize the problem is (2,000,4,000)