Question

Find the solutions to the system of equations. Select all that apply.

Y=x^2-4
Y=-2x-5

A. (-2,0)
B. (-5,0)
C. (2,0)
D. (-1,-3)

Answer 1

Answer: Hello there!

The system of equation given is:

y = x^2-4

y = -2x-5

And we want to solve this system:

the first step we can do is replace y in the first equation by the given in the second equation:

y = x^2-4 = -2x - 5

now we can solve it for x:

x^2-4 +2x + 5 = 0

x^2 +2x + 1 = 0

and now we can use the cuadratic equation forumla:

this is, if we have a function of the form:

ax^2 + bx + c = 0

the solutions are:

`x = (-b +/- √(b^2 -4ac) )/(2a)`

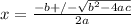
in our equation we have a=1, b = 2 and c= 1

we replace it in the formula given, and we obtain:

`x = (-2 +/- √(2^2 -4*(1)) )/(2) = (-2 +/- √(4 - 4) )/(2) = -2/2 = -1`

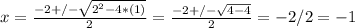
Now we got the value of x, and we could replace it in one of the equations and get the value of y:

y = -2x-5

y = -2*(-1) - 5 = 2 -5 = -3

then the pair is (-1, -3)

and the correct option is D.

Answer 2

D. (-1, -3)

Explanation:

`\left\{\begin{array}{ccc}y=x^2-4&(1)\\y=-2x-5&(2)\end{array}\right\\\\\text{Put (1) to (2):}\\\\x^2-4=-2x-5\qquad\text{add}\ 2x\ \text{and 5 to both sides}\\\\x^2+2x+1=0\\\\x^2+x+x+1=0\\\\x(x+1)+1(x+1)=0\\\\(x+1)(x+1)=0\\\\(x+1)^2=0\iff x+1=0\qquad\text{subtract 1 from both sides}\\\\x=-1\\\\\text{put the value of}\ x\ \text{to}\ (2):\\\\y=-2(-1)-5\\\\y=2-5\\\\y=-3`