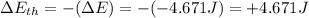Question

A cart is attached to a string and the other end of the string is attached to a weight that is free to fall. The cart is initially released from rest, and travels a distance of 0.521 m m before hitting a stopper. The cart's final speed was 0.931 m/s . The inertia of the weight is 0.115 kg , while the inertia of the cart is 1.000 kg . For the next 4 parts consider a system of the earth, the weight, the cart, the string, and the track. Assume the track does not move relative to the earth.1- What is the final speed of the weight?2- What is the change in kinetic energy of the system?3- What is the change in potential energy of the system?4- What is the change in thermal energy of the system due to friction?

Answer 1

1. 3.20 m/s

Assuming the string is inextensible, the cart and the weight travels the same distance: so, since the cart travels for 0.521 m, the distance travelled by the weigth is the same:

d = 0.521 m

The motion of the weigth is a free-fall motion with acceleration g = 9.8 m/s^2, so its final speed can be found by using the equation

`v^2 = u^2 + 2gd`

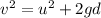
where

u = 0

is the initial speed of the weigth (at rest). Substituting into the formula, we find

`v=√(0+2(9.8 m/s^2)(0.521 m))=3.20 m/s`

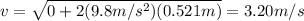
2. 1.022 J

The change in kinetic energy of the system is equal to the sum of the kinetic energies acquired by the cart and the weight. They both started from rest, so their initial kinetic energies were zero.

The cart has

mass: m = 1.000 kg

final speed: v = 0.931 m/s

so its gained kinetic energy is

`K_c = (1)/(2)mv^2=(1)/(2)(1.000 kg)(0.931 m/s)^2=0.433 J`

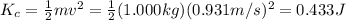
The weight has

mass: m = 0.115 kg

final speed: v = 3.20 m/s

so its gained kinetic energy is

`K_w = (1)/(2)mv^2=(1)/(2)(0.115 kg)(3.20 m/s)^2=0.589 J`

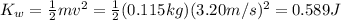
So the change in kinetic energy of the system is

`\Delta K= K_f - K_i = (0.433 J+0.589 J)-0=1.022 J`

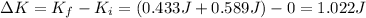
3. -5.693 J

The potential energy of the falling cart decreases by the following amount:

`\Delta U = mg \Delta h`

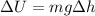
where

m = 1.000 kg is the mass

g = 9.8 m/s^2

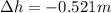`\Delta h = -0.521 m` is the change in height of the cart

Substituting, we find

`\Delta U=(1.000 kg)(9.8 m/s^2)(-0.521 m)=-5.106 J`

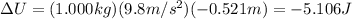
the potential energy of the falling weight decreases by the following amount:

`\Delta U = mg \Delta h`

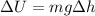
where

m = 0.115 kg is the mass

g = 9.8 m/s^2

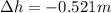`\Delta h = -0.521 m` is the change in height of the weight (calculated at point a)

Substituting, we find

`\Delta U=(0.115 kg)(9.8 m/s^2)(-0.521 m)=-0.587 J`

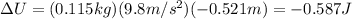
So, the change in potential energy is

`\Delta U = -5.106 J-0.587 J=-5.693 J`

4. +4.671 J

The change in thermal energy of the system due to friction is equal to the loss in mechanical energy of the system.

The system has gained a kinetic energy equal to

`\Delta K=+1.022 J`

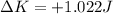
while it has lost a potential energy equal to

`\Delta U =-5.693 J`

So the loss in mechanical energy of the system is

`\Delta E=\Delta K+\Delta U=+1.022 J-5.693 J=-4.671 J`

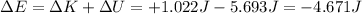
So the change in termal energy is

`\Delta E_(th) = -(\Delta E)=-(-4.671 J)=+4.671 J`