Question

A farmer wants to build a rectangular pen with 80 feet of fencing. The pen will be built against the wall of the barn so one side of the rectangle won’t need a fence. What dimensions will maximize the area of the pen?

Answer 1

length is 40

Width is 20

Explanation:

Answer 2

The length of the rectangular pen is
`40\ ft`

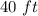
The width of the rectangular pen is
`20\ ft`

Explanation:

Let

x-----> the length of the rectangular pen

y----> the width of the rectangular pen

we know that

The perimeter of the rectangular pen in this problem is equal to

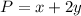`P=x+2y` ---> remember that one side of the rectangle won’t need a fence

`P=80\ ft`

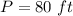
so

`80=x+2y`

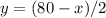`y=(80-x)/2` -----> equation A

The area of the rectangular pen is equal to

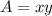`A=xy` -----> equation B

Substitute equation A in equation B

`A=x*(80-x)/2\\ \\A=-0.5x^(2)+40x`

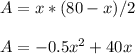
The quadratic equation is a vertical parabola open downward

The vertex is a maximum

The x-coordinate of the vertex is the length of the rectangular pen that maximize the area of the pen

The y-coordinate of the vertex is the maximum area of the pen

using a graphing tool

The vertex is the point (40,800)

see the attached figure

so

`x=40\ ft`

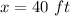
Find the value of y

`y=(80-x)/2` ---->
`y=(80-40)/2=20\ ft`

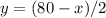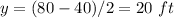
therefore

The length of the rectangular pen is
`40\ ft`

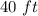
The width of the rectangular pen is
`20\ ft`