Answer:
Part 4)
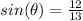
Part 10) The angle of elevation is
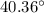
Part 11) The angle of depression is
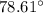
Part 12)
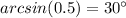 or
or
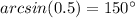
Part 13)
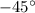 or
or
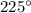
Explanation:
Part 4) we have that
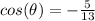
The angle theta lies in Quadrant II
so
The sine of angle theta is positive
Remember that
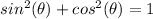
substitute the given value
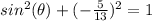
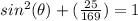
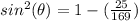
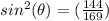
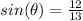
Part 10)
Let
 ----> angle of elevation
----> angle of elevation
we know that
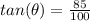 ----> opposite side angle theta divided by adjacent side angle theta
----> opposite side angle theta divided by adjacent side angle theta
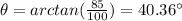
Part 11)
Let
 ----> angle of depression
----> angle of depression
we know that
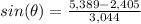 ----> opposite side angle theta divided by hypotenuse
----> opposite side angle theta divided by hypotenuse
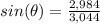
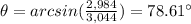
Part 12) What is the exact value of arcsin(0.5)?
Remember that

therefore
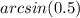 -----> has two solutions
-----> has two solutions
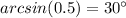 ----> I Quadrant
----> I Quadrant
or
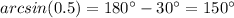 ----> II Quadrant
----> II Quadrant
Part 13) What is the exact value of
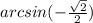
The sine is negative
so
The angle lies in Quadrant III or Quadrant IV
Remember that
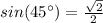
therefore
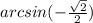 ----> has two solutions
----> has two solutions
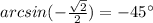 ----> IV Quadrant
----> IV Quadrant
or
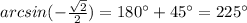 ----> III Quadrant
----> III Quadrant