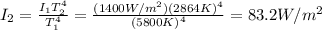Answer:
83.2 W/m^2
Step-by-step explanation:
The radiation per unit area of a star is directly proportional to the power emitted, which is given by Stefan-Boltzmann law:
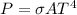
where
 is the Stefan-Boltzmann constant
is the Stefan-Boltzmann constant
A is the surface area
T is the surface temperature
So, we see that the radiation per unit area is proportional to the fourth power of the temperature:
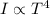
So in our problem we can write:
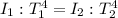
where
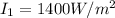 is the power per unit area of the present sun
is the power per unit area of the present sun
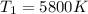 is the temperature of the sun
is the temperature of the sun
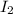 is the power per unit area of sun X
is the power per unit area of sun X
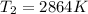 is the temperature of sun X
is the temperature of sun X
Solving for I2, we find