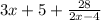Question

The height of a rectangular prism is found by dividing volume, V, by the base area, B.

If the volume of the rectangular prism is represented by 6x2 – 2x + 8 and the base area is 2x – 4, which expression represents the height?

Answer 1

`3x+5 + (28)/(2x-4)`

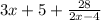
Explanation:

If the volume of the rectangular prism is represented by
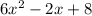`6x^2 - 2x + 8` and the base area is
`2x - 4`

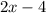
Volume of a prism = base area times height

we replace the volume and the base area

`6x^2-2x+8 = (2x-4) \cdot height`

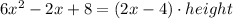
Divide both sides by 2x-4

`height= (6x^2-2x+8)/(2x-4)`

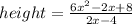
we use long division.

3x+5

----------------------------------------------

`2x-4`
`6x^2 - 2x + 8`

`6x^2 - 12x`

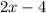
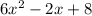
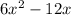
-----------------------------------------------(subtract)

`10x+8`

`10x-20`

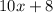
------------------------------------------------(subtract)

28

`3x+5 + (28)/(2x-4)`