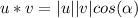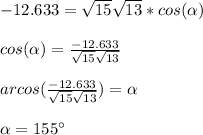Question

Find the angle between vector u=2i+sqrt(11)j and v=-3i-2j to the nearest degree

Answer 1

Answer: Last option 155°

Explanation:

We have the components of the vectors u and v.

Then, to find the angle between them, perform the following steps:

1) Calculate the scalar product u * v

If
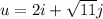`u = 2i + √(11)j` and
`v = -3i-2j`

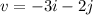
Then, the product scalar u * v is:

`u * v = (2)(-3) + (√(11))(-2)`

`u * v = -6-2√(11)`

`u * v = -12.633`

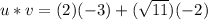
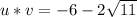
2) Calculation of the magnitude of both vectors.

`| u | = \sqrt{(2) ^ 2 + (√(11))^2}\\\\| u | = √(4+11)\\\\| u | = √(15)`

`| v | = √((- 3) ^ 2 + (- 2) ^ 2)\\\\| v | = √(9 +4)\\\\| v | = √(13)`

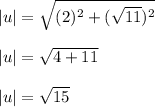
3) Now that you know the product point between the two vectors and the magnitude of each, then use the following formula to find an angle

`u * v = | u || v |cos(\alpha)`

`-12.633 = √(15)√(13)*cos(\alpha)\\\\cos(\alpha) = (-12.633)/(√(15)√(13))\\\\arcos((-12.633)/(√(15)√(13))) = \alpha\\\\\alpha =155\°`