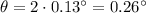Question

In conventional television, signals are broadcast from towers to home receivers. Even when a receiver is not in direct view of a tower because of a hill or building, it can still intercept a signal if the signal diffracts enough around the obstacle, into the obstacle’s “shadow region.” Current television signals have a wavelength of about 54 cm, but future digital television signals that are to be transmitted from towers will have a wavelength of about 13 mm. (a) Did this change in wavelength increase or decrease the diffraction of the signals into the shadow regions of obstacles? Assume that a signal passes through an opening of 5.7 m width between two adjacent buildings. What is the angular spread of the central diffraction maximum (out to the first minima) for wavelengths of (b) 54 cm and (c) 13 mm?

Answer 1

(a) The diffraction decreases

The formula for the diffraction pattern from a single slit is given by:

`sin \theta = (n \lambda)/(a)`

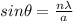
where

`\theta` is the angle corresponding to nth-minimum in the diffraction pattern, measured from the centre of the pattern

n is the order of the minimum

`\lambda` is the wavelength

a is the width of the opening

As we see from the formula, the longer the wavelength, the larger the diffraction pattern (because
`\theta` increases). In this problem, since the wavelength of the signal has been decreased from 54 cm to 13 mm, the diffraction of the signal has decreased.

(b)
`10.8^(\circ)`

The angular spread of the central diffraction maximum is equal to twice the distance between the centre of the pattern and the first minimum, with n=1. Therefore:

`sin \theta = ((1) \lambda)/(a)`

in this case we have

`\lambda=54 cm = 0.54 m` is the wavelength

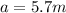`a=5.7 m` is the width of the opening

Solving the equation, we find

`\theta = sin^(-1) ((\lambda)/(a))=sin^(-1) ((0.54 m)/(5.7 m))=5.4^(\circ)`

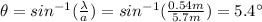
So the angular spread of the central diffraction maximum is twice this angle:

`\theta = 2 \cdot 5.4^(\circ)=10.8^(\circ)`

(c)
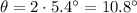
`0.26^(\circ)`

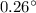
Here we can apply the same formula used before, but this time the wavelength of the signal is

`\lambda=13 mm=0.013 m`

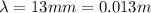
so the angle corresponding to the first minimum is

`\theta = sin^(-1) ((\lambda)/(a))=sin^(-1) ((0.013 m)/(5.7 m))=0.13^(\circ)`

So the angular spread of the central diffraction maximum is twice this angle:

`\theta = 2 \cdot 0.13^(\circ)=0.26^(\circ)`