Answer:
The correct is B)

Explanation:
In provided graph f(x) is x² which is equation of parabola
this is shown by blue graph
we need to find the equation of red graph which is denoted by g(x)
It can be seen from graph that g(x) is downward so, in this equation coefficient must be in negative.
In part A)

so,
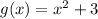
here is not negative coefficient
In part B)

here is negative coefficient
This shows downward direction of parabola.
and negative 3 shows the shifting of parabola downward by 3 units.
Hence, this condition matches only option B)

In part C)
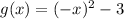
so,
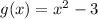
here is not negative coefficient
In part D)

since, here is negative coefficient
This shows downward direction of parabola.
and positive 3 shows the shifting of parabola upward by 3 units.
So, the correct is B)
