Question

A solid sphere of uniform density has a mass of 4.4 × 104 kg and a radius of 1.9 m. What is the magnitude of the gravitational force due to the sphere on a particle of mass 8.3 kg located at a distance of (a) 3.7 m and (b) 0.41 m from the center of the sphere? (c) Write a general expression for the magnitude of the gravitational force on the particle at a distance r ≤ 1.9 m from the center of the sphere.

Answer 1

(a)
`1.78\cdot 10^(-6)N`

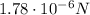
Here we want to find the gravitational force exerted on the particle at a distance of 3.7 m from the center of the sphere. Since the radius of the sphere is 1.9 m, we are outside the sphere, so we can use Newton's law of gravitation:

`F=G(mM)/(r^2)`

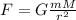
where

G is the gravitational constant

m = 8.3 kg is the mass of the particle

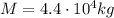`M=4.4\cdot 10^4 kg` is the mass of the sphere

r = 3.7 m is the distance

Substituting into the formula, we find

`F=(6.67\cdot 10^(-11))((8.3 kg)(4.4\cdot 10^4 kg))/((3.7 m)^2)=1.78\cdot 10^(-6) N`

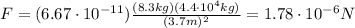
(b)
`1.46\cdot 10^(-6)N`

Here we want to find the gravitational force exerted on the particle at a distance of 0.41 m from the center of the sphere. Since the radius of the sphere is 1.9 m, this time we are inside the sphere, so the formula for the gravitational force is different:

`F=G(mMr)/(R^3)`

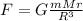
where

G is the gravitational constant

m = 8.3 kg is the mass of the particle

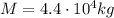`M=4.4\cdot 10^4 kg` is the mass of the sphere

r = 0.41 m is the distance from the centre of the sphere

R = 1.9 m is the radius of the sphere

Substituting numbers into the formula, we find

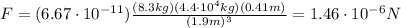
`F=(6.67\cdot 10^(-11))((8.3 kg)(4.4\cdot 10^4 kg)(0.41 m))/((1.9 m)^3)=1.46\cdot 10^(-6)N`

(c)
`F=G(mMr)/(R^3)`

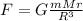
The magnitude of the gravitational force on the particle when located inside the sphere can be found starting from Newton's law of gravitation:

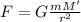`F=G(mM')/(r^2)` (1)

where the only difference compared to the standard law is that M' is not the total mass of the sphere, but only the amount of mass of the sphere enclosed by the spherical surface of radius r centered in the center of the sphere.

The mass enclosed is

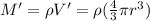`M'=\rho V' = \rho ((4)/(3)\pi r^3)` (2)

where
`\rho` is the density of the sphere and V' is the enclosed volume. We can rewrite the density of the sphere as ratio between mass of the sphere (M) and volume of the sphere:

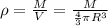`\rho=(M)/(V)=(M)/((4)/(3)\pi R^3)` (3)

where R is the radius of the sphere.

Substituting (3) into (2):

`M' = ((M)/((4)/(3)\pi R^3)) ((4)/(3)\pi r^3)=(Mr^3)/(R^3)`

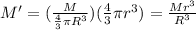
And substituting the last equation into (1), we find

`F=G(m((Mr^3)/(R^3)))/(r^2)=G(mMr)/(R^3)`

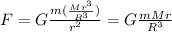
which depends linearly on r.