Question

Use the table below to find (f o g)(1)

Answer 1

F(G(2))=23

Explanation:

To solve this problem we need to find the equation from each line, then find the expression for the composite function F(G(X)) and finally evaluate it in x=2.

The given functions behave like lines, hence we will use an approach of the same matter.

F(x)=ax+b where, 'a' is the slope and b the interception with 'y'=axis

G(x)=cx+d where, 'c' is the slope and d the interception with 'y'=axis

Using the first point (x=0) we will obtain 'b' and 'd'.

F(0)=a*0+b=5, we have b=5

G(0)=c*0+d=3, we have d=3

To obtain the slope of every function we need to use the equation for slopes

`m=(y_(2)-y_(1))/(x_(2)-x_(1))`

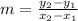
Where (x1,y1)=(0,5) and (x2,y2)=(1,7) for F(x) and (x1,y1)=(0,3) and (x2,y2)=(1,6) for G(x)

Using the above equation, we have that a= 2 and c=3

Hence

F(x)= 2x+5

G(x)=3x+3

Now the composite function is obtained by replacing 'x' inside F(x) by G(x)

F(G(x))=6x+6+5

Evaluating in x=2

F(G(2))=6*2+11=23