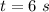Question

.

A ball is thrown into the air with an initial velocity of 80 ft/sec. The height of the ball after t seconds in the air is given by h(t) =-16t^2 + 80t + 96.How long will it take for the ball land on the ground? (When will the height equal 0?)

Answer 1

After 5 seconds

Explanation:

Have a great day

Answer 2

`t= 6\ s`

Explanation:

We know that the equation that models the height of the ball as a function of time is
`h(t) = -16t ^ 2 + 80t + 96`.

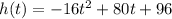Where the initial speed is 80 feet.

When the ball lands on the ground, its height will be
`h(t) = 0`.

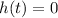So to know how long it will take the ball to reach the ground, equal h (t) to zero and solve for t.

`-16t ^ 2 + 80t + 96 = 0`

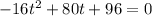
To solve this quadratic equation we use the quadratic formula.

For an equation of the form:

`at^2 +bt +c`

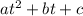
The quadratic formula is:

`t=(-b\±√(b^2 -4ac))/(2a)`

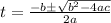
In this case

`a =-16\\b = 80\\c =96`

Then

`t=(-80\±√(80^2 -4(-16)(96)))/(2(-16))`

`t_1=-1\\\\t_2=6`

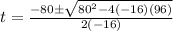
We take the positive solution

`t= 6\ s`