Answer:
The x-intercepts are (4,0) and (-9,0)
Explanation:
We want to find the x-intercepts of the function:
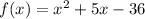
At x-intercept,
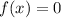
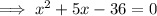
We split the middle term to obtain;
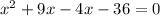
Factor by grouping:
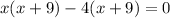
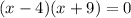
Apply the zero product principle.
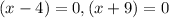
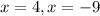
Hence the x-intercepts are (4,0) and (-9,0)