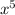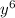Question

Write the product of the monomials (8x6y)2 and (x3y4).

Answer 1

The product of the monomials is 2304
`x^(5)`
`y^(6)`

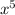
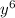
Explanation:

* Lets explain how to solve the problem

- We need to find the product of the monomials (8x 6y)² and

`x^(3)y^(4)`

- At first lets solve the power of the first monomial

- Because the power 2 is on the bracket then each element inside the

bracket will take power 2

∵ (8x 6y)² = (8)²(x)²(6)²(y)²

∵ (8)² = 64

∵ (x)² = x²

∵ (6)² = 36

∵ (y)² = y²

∴ (8x 6y)² = [64x² × 36y²]

∵ 64 × 36 = 2304 x²y²

∴ The first monomial is 2304 x²y²

∵ The first monomial is 2304 x²y²

∵ The second monomial is
`x^(3)y^(4)`

- Lets find their product

- Remember in multiplication if two terms have same bases then we

will add their powers

∵ [2304 x²y²] × [
`x^(3)y^(4)` ] =

2304 [
`x^(2)*x^(3)` ] [
`y^(2)*y^(4)` ]

∵
`x^(2)*x^(3)` =
`x^(2+3)` =
`x^(5)`

∵
`y^(2)*y^(4)` =
`y^(2+4)` =
`y^(6)`

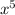
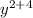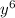
∴ [2304 x²y²] × [
`x^(3)y^(4)` ] = 2304
`x^(5)`
`y^(6)`

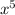
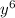
The product of the monomials is 2304
`x^(5)`
`y^(6)`