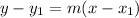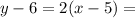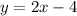Question

Find an equation of the tangent to the curve x =5+lnt, y=t2+5 at the point (5,6) by both eliminating the parameter and without eliminating the parameter.

Answer 1

`y = 2x -4`

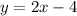
Step-by-step explanation

Part a)

Eliminating the parameter:

The parametric equation is

`x = 5 + ln(t)`

`y = {t}^(2) + 5`

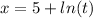
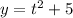
From the first equation we make t the subject to get;

`x - 5 = ln(t)`

`t = {e}^(x - 5)`

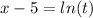
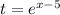
We put it into the second equation.

`y = { ({e}^(x - 5)) }^(2) + 5`

`y = { ({e}^(2(x - 5))) } + 5`

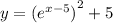
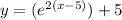
We differentiate to get;

`(dy)/(dx) = 2 {e}^(2(x - 5))`

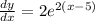
At x=5,

`(dy)/(dx) = 2 {e}^(2(5 - 5))`

`(dy)/(dx) = 2 {e}^(0) = 2`

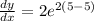
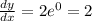
The slope of the tangent is 2.

The equation of the tangent through

(5,6) is given by

`y-y_1=m(x-x_1)`

`y - 6 = 2(x - 5)`

`y = 2x - 10 + 6`

`y = 2x -4`

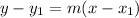
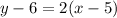
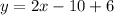
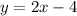
Without eliminating the parameter,

`(dy)/(dx) = ( (dy)/(dt) )/( (dx)/(dt) )`

`(dy)/(dx) = ( 2t)/( (1)/(t) )`

`(dy)/(dx) = 2 {t}^(2)`

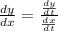
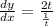
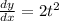
At x=5,

`5 = 5 + ln(t)`

`ln(t) = 0`

`t = {e}^(0) = 1`

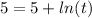
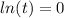
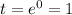
This implies that,

`(dy)/(dx) = 2 {(1)}^(2) = 2`

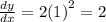
The slope of the tangent is 2.

The equation of the tangent through

(5,6) is given by

`y-y_1=m(x-x_1)`

`y - 6 = 2(x - 5) =`

`y = 2x -4`