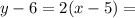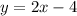ANSWER
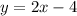
Step-by-step explanation
Part a)
Eliminating the parameter:
The parametric equation is
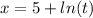
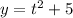
From the first equation we make t the subject to get;
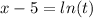
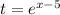
We put it into the second equation.
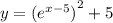
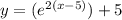
We differentiate to get;
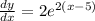
At x=5,
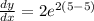
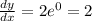
The slope of the tangent is 2.
The equation of the tangent through
(5,6) is given by


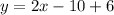
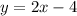
Without eliminating the parameter,

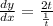
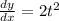
At x=5,
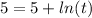
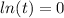
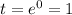
This implies that,
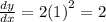
The slope of the tangent is 2.
The equation of the tangent through
(5,6) is given by