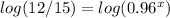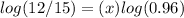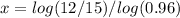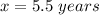Answer:
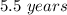
Explanation:
we know that
In this problem we have a exponential function of the form
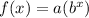
where
x is the time in years
f(x) is the value of the stock
a is the initial value
b is the base
r is the rate
b=(1-r)
we have
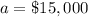

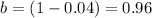
substitute
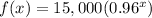
80% of original price is equal to
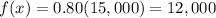
so
For f(x)=12,000 ------> Find the value of x
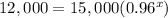

Apply log both sides