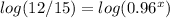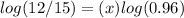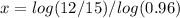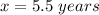Question

Mr Turner bought stock for $15,000. If the value of the stock decreases 4% each year when will it be worth 80% of original price?

Answer 1

`5.5\ years`

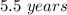
Explanation:

we know that

In this problem we have a exponential function of the form

`f(x)=a(b^(x))`

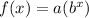
where

x is the time in years

f(x) is the value of the stock

a is the initial value

b is the base

r is the rate

b=(1-r)

we have

`a=\$15,000`

`r=4\%=4/100=0.04`

`b=(1-0.04)=0.96`

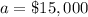
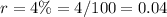
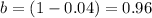
substitute

`f(x)=15,000(0.96^(x))`

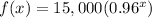
80% of original price is equal to

`f(x)=0.80(15,000)=12,000`

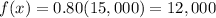
so

For f(x)=12,000 ------> Find the value of x

`12,000=15,000(0.96^(x))`

`(12/15)=(0.96^(x))`

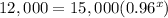
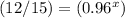
Apply log both sides

`log(12/15)=log(0.96^(x))`

`log(12/15)=(x)log(0.96)`

`x=log(12/15)/log(0.96)`

`x=5.5\ years`