Question

What transformation has changed the parent function f(x) = (.5)x to its new appearance shown in the graph below?

exponential graph passing through point negative 1, negative 2 and point 0, negative 1.

f(x) − 2
2 • f(x)
f(x) + 1
−1 • f(x)

Answer 1

f(x) -2 is the correct answer.

Explanation:

Just took the test!

Answer 2

Last option

−1 • f(x)

Explanation:

The function
`f(x) = (0.5) ^ x` passes through point (-1, 2) because:

`f(-1) = (0.5) ^ {-1}= (1)/((0.5)) = 2`

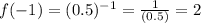
and also goes through the point (0, 1)

Because:

`f(0) = (0.5)^0 = 1`

Then, if the transformed function passes through the point (0, -1) and passes through the point (-1, -2) then this means that the graph of
`f(x) = (0.5) ^ x` reflected on the axis x. This means that if the point
`(x_0, y_0)` belongs to f(x), then the point
`(x_0, -y_0)` belongs to the transformed function

The transformation that reflects the graph of a function on the x-axis is.

`y = cf(x)`

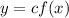
Where c is a negative number. In this case
`c = -1`

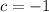
Then the transformation is:

`y = -1*f(x)`

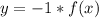
and the transformed function is:

`f (x) = - (0.5) ^ x`

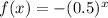
Observe the attached image.