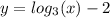Answer: Third option
Explanation:
The function
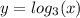 passes through the point (1,0) since the function
passes through the point (1,0) since the function
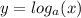 always cuts the x-axis at
always cuts the x-axis at
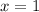 .
.
Then, if the transformed function passes through point (1,-2) then this means that the graph of
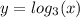 was moved vertically 2 units down.
was moved vertically 2 units down.
The transformation that displaces the graphically of a function k units downwards is:
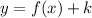
Where k is a negative number. In this case
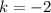
Then the transformation is:
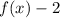
and the transformed function is: