Answer:
The equation is:
72 = (b - 1)*b = b^2 - b
And the solution to this problem is:
b = 9
So we have 9 bottles in each one of the longer rows.
Explanation:
Let's use the variables:
b = number of bottles in the longer rows
a = number of bottles in the shorter rows.
We know that the total number of bottles in the crate will be equal to the product between a and b.
then:
72 = a*b
And we also know that
"e rows across the width of the crate hold 1 bottle less than the rows across the length of the crate."
This means that
a = b - 1
Now, we could replace this in the above equation to get:
72 = (b - 1)*b = b^2 - b
Then we have the quadratic equation:
b^2 - b - 72 = 0
The solutions of this equation can be found if we use Bhaskara's formula, the two solutions are:
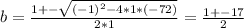
Then we have two solutions:
b = (1 - 17)/2 = -16/2 = -8 (this is a negative number, and has no meaning in our case, then this solution can be discarded)
the other solution is:
b = (1 + 17)/2 = 18/2 = 9
This is our solution, the larger rows have 9 bottles each.