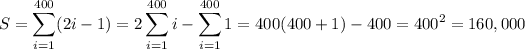Question

2. Determine the sum of the first 400 ODD numbers.

​

Answer 1

Odd numbers take the form
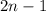`2n-1`, where
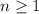`n\ge1` is an integer. When
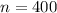`n=400`, the last odd number would be 799. So we're adding

`S=1+3+5+\cdots+795+797+799`

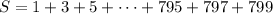
By reversing the order of terms, we have

`S=799+797+795+\cdots+5+3+1`

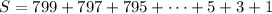
and we can pair up terms in both sums at the same position to write

`2S=(1+799)+(3+797)+(5+795)+\cdots(795+5)+(797+3)+(799+1)`

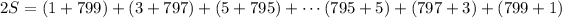
so that we are basically adding 400 copies of 800, and from there we can find the value of the sum right away:

`2S=400\cdot800\implies S=160,000`

###

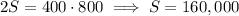
We could also make use of the formulas,

`\displaystyle\sum_(i=1)^n1=n`

`\displaystyle\sum_(i=1)^ni=\frac{n(n+1)}2`

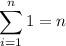
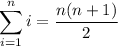
We have

`S=\displaystyle\sum_(i=1)^(400)(2i-1)=2\sum_(i=1)^(400)i-\sum_(i=1)^(400)1=400(400+1)-400=400^2=160,000`