Question

The parent function f(x) = x2 is translated such that the function g(x) = –x2 + 6x – 5 represents the new function.

What is true about the transformation that was performed? Check all that apply.
g(x) has an axis of symmetry at x = 3.
g(x) is shifted down 5 units from the graph of f(x).
g(x) is shifted right 3 units from the graph of f(x).
g(x) is shifted up 4 units from the graph of f(x).
g(x) is narrower than f(x).

Answer 1

Explanation:

on edge its A,C,D :)

Answer 2

g(x) has an axis of symmetry at x = 3.

g(x) is shifted right 3 units from the graph of f(x)

g(x) is shifted up 4 units from the graph of f(x).

Explanation:

The parent function is:

`f(x)=x^2`

The transformed function is
`g(x)=-x^2+6x-5`.

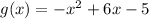This new function can be rewritten in the vertex form as:

`g(x)=-(x-3)^2+4`

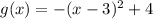
This function is obtained by shifting the parent function 3 units right and 4 units up.

The axis of symmetry is x=3;(x=h) and h=3.

There is no horizontal stretch or compression.

The new function is however reflected in the x-axis