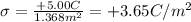Question

A thick, spherical shell made of solid metal has an inner radius a = 0.18 m and an outer radius b = 0.33 m, and is initially uncharged. A point charge q = 5.00 C is placed at the center of the shell. What is the electric field strength in the region r < a? Express your answer in terms of 1/r2. Tries 0/8 What is the electric field strength in the region a < r < b? Express your answer in terms of 1/r2. Tries 0/8 What is the electric field strength in the region b < r? Express your answer in terms of 1/r2. Tries 0/8 What is the induced charge density at r = a? (in C/m^2) Tries 0/8 What is the induced charge density (in C/m2) at r = b? (in C/m^2)

Answer 1

A)
`E=(4.50\cdot 10^(10))/(r^2) V/m`

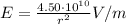
r < a

We can find the magnitude of the electric field by using Gauss theorem. Taking a Gaussian spherical surface of radius r centered in the centre of the sphere, the electric flux through the surface of the sphere is equal to the ratio between the charge contained in the sphere and the vacuum permittivity:

`E\cdot 4 \pi r^2 = (q)/(\epsilon_0)`

For r < a, the charge contained in the gaussian sphere is the point charge:

`q=5.00 C`

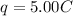
So the electric field in this region is

`E=(q)/(4\pi \epsilon_0 r^2)=(5.00 C)/(4\pi (8.85\cdot 10^(-12) F/m))(1)/(r^2)=(4.50\cdot 10^(10))/(r^2) V/m`

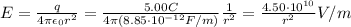
B) E = 0

a < r < b

The region a < r < b is the region between the inner and the outer surface of the shell. We have to keep in mind that the presence of the single point charge +q = 5.00 C at the center of the sphere induces an opposite charge -q on the inner surface (r=a), and a charge of +q at the outer surface (r=b).

Using again Gauss theorem

`E\cdot 4 \pi r^2 = (q')/(\epsilon_0)`

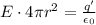
this time we have that the gaussian sphere contains both the single point charge +q and the negative charge -q induced at r=a, so the net charge contained in the sphere is

q' = +q - q = 0

And so, the electric field in this region is zero.

C)
`E=(4.50\cdot 10^(10))/(r^2) V/m`

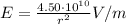
r > b

Here we are outside of the sphere. Using Gauss theorem again

`E\cdot 4 \pi r^2 = (q')/(\epsilon_0)`

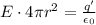
this time we have that the gaussian sphere contains the single point charge +q, the negative charge -q induced at r=a, and the positive charge +q induced at r=b, so the net charge contained in the sphere is

q' = +q - q +q = q

And so the electric field is identical to the one inside the sphere:

`E=(q)/(4\pi \epsilon_0 r^2)=(5.00 C)/(4\pi (8.85\cdot 10^(-12) F/m))(1)/(r^2)=(4.50\cdot 10^(10))/(r^2) V/m`

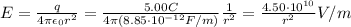
D) -12.29 C/m^2

We said that the charge induced at the inner surface r=a is

-q = -5.00 C

The induced charge density is

`\sigma = (-q)/(A)`

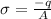
where A is the area of the inner surface of radius r = a = 0.18 m, so it is

`A=4\pi a^2 = 4 \pi (0.18 m)^2=0.407 m^2`

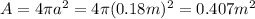
So the induced charge density is

`\sigma = (-5.00 C)/(0.407 m^2)=-12.29 C/m^2`

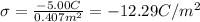
E) +3.65 C/m^2

We said that the charge induced at the outer surface r=b is

+q = +5.00 C

The induced charge density is

`\sigma = (+q)/(A)`

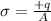
where A is the area of the outer surface of radius r = b = 0.33 m, so it is

`A=4\pi b^2 = 4 \pi (0.33 m)^2=1.368 m^2`

So the induced charge density is

`\sigma = (+5.00 C)/(1.368 m^2)=+3.65 C/m^2`