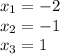Question

What are the real zeros of the function g(x) = x3 + 2x2 − x − 2?

Answer 1

For this case, to find the roots of the function, we equate to zero.

`x ^ 3 + 2x ^ 2-x-2 = 0`

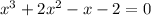
We rewrite how:

`x ^ 3 + 2x ^ 2- (x + 2) = 0`

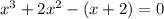
We factor the maximum common denominator of each group:

`x ^ 2 (x + 2) -1 (x + 2) = 0`

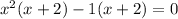
We factor the polynomial, factoring the maximum common denominator
`(x + 2):`

`(x + 2) (x ^ 2-1) = 0`

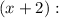
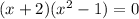
By definition of perfect squares we have to:

`a ^ 2-b ^ 2 = (a + b) (a-b)`

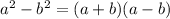
ON the expression
`(x ^ 2-1):`

`a = x\\b = 1`

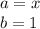
So:

`(x ^ 2-1) = (x + 1) (x-1)`

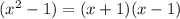
Thus, the factorization of the polynomial is:

`(x + 2) (x + 1) (x-1) = 0`

`x_ {1} = - 2\\x_ {2} = - 1\\x_ {3} = 1`

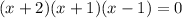
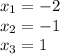
ANswer:
`x_ {1} = - 2\\x_ {2} = - 1\\x_ {3} = 1`