Question

On coordinate axes, point A = (1.50, 2.00), measured in meters. Let the voltage value very far away (“infinity”) be defined as zero (i.e. V∞ = 0). To make things simpler, just express your answers in terms of e and k (in other words, don’t plug in numerical values for e and k). A lone proton is placed at the origin: a. Calculate the electric field (magnitude and direction) it will cause at point A. b. Calculate the magnitude and direction of the electric force it will exert on a proton located at point A. c. Calculate the magnitude and direction of the electric force it will exert on an electron located at point A. d. Calculate the uniform electric field (magnitude and direction) that would need to be present (in addition to the proton), so that an electron located at point A would have no acceleration. e. Calculate the electric potential (i.e. the voltage) that the lone proton will cause at point A. f. Calculate the electric potential energy (UE) that a second proton would have if located at point A. g. Calculate the electric potential energy (UE) that an electron would have if located at point A.

Answer 1

a.
`E=k(e)/(6.25)`,
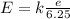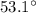`53.1^(\circ)` above x-axis

The electric field produced by a single point charge is

`E=k(q)/(r^2)`

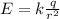
where

q is the charge

r is the distance from the charge

In this case,

q = e

the charge is at the origin, so the distance of point A (1.50, 2.00) from the charge is

`r=√((1.50-0)^2+(2.00-0)^2)=2.5`

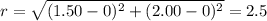
So the magnitude of the electric field at point A is

`E=k(e)/((2.5)^2)=k(e)/(6.25)`

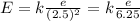
The electric field produced by a single-point positive charge is radial, pointing away from the charge. So the direction of the field in this case is given by

`\theta = tan^(-1) ((A_y)/(A_x))=tan^(-1) ((2.00)/(1.50))=53.1^(\circ)`

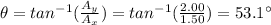
above the x-axis.

b.
`F=k(e^2)/(6.25)`,
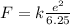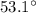`53.1^(\circ)` above x-axis

The magnitude of the electric force exerted on a charge is given by

`F=qE`

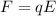
where

q is the charge magnitude

E is the electric field strength

In this case, we have a proton (charge e), and the electric field strength at point A is

`E=k(e)/(6.25)`

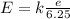
So the force exerted on the proton is

`F=(e)(k(e)/(6.25))=k(e^2)/(6.25)`

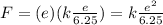
Moreover, the direction of the electric force exerted on a positive charge is equal to the direction of the electric field at that point, so the direction of the electric force is also
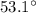`53.1^(\circ)` above x-axis.

c.
`F=k(e^2)/(6.25)`,
`233.1^(\circ)`

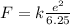The electric force exerted on a charge is given by

`F=qE`

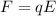
In this case, we have an electron (charge e), and the electric field strength at point A is

`E=k(e)/(6.25)`

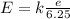
So the force exerted on the electron is equal as the one for the proton:

`F=(e)(k(e)/(6.25))=k(e^2)/(6.25)`

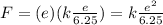
However, this time the direction is different: in fact, for a negative charge the electric force points in a direction opposite to the electric field. So, the direction of the electric force in this case is

`\theta = 53.1^(\circ)+180^(\circ)=233.1^(\circ)`

d.
`E'=k(e)/(6.25)`,
`233.1^(\circ)`

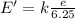In order for the electron at point A not to have acceleration, the net force on it should be zero:

`F_(net) =0`

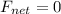
The net force is the algebraic sum of the force calculated at point c), due to the electric field produced by the proton, and the additional force F' due to the uniform electric field that we need to add:

`F_(net)=F+F' = 0\\F' = -F`

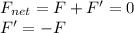
Rewriting
`F'=eE'`

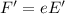
where E' is the uniform electric field that we add, we find

`E' = -(F)/(e)=-(1)/(e)k(e^2)/(6.25)=-k(e)/(6.25)\\`

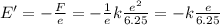
So the magnitude of the uniform electric field must be

`E'=k(e)/(6.25)`

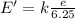
and the direction must be opposite to the electric field produced by the proton, so at an angle of
`233.1^(\circ)`.

e.
`V=k (e)/(2.5)`

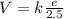
The electric potential generated by a single-point positive charge is

`V=k (q)/(r)`

where here we have

q = e is the charge of the proton

r = 2.5 is the distance of point A from the proton

Substituting into the formula, we find

`V=k (e)/(2.5)`

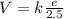
f.
`k(e^2)/(2.5)`

The electric potential energy of a charge in an electric field is

`U=qV`

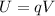
where q is the charge and V is the electric potential

Here we have a proton (charge q=e) located at point A, where the potential is

`V=k (e)/(2.5)`

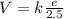
So its electric potential energy is

`U=(e)(k(e)/(2.5))=k(e^2)/(2.5)`

g.
`-k(e^2)/(2.5)`

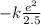
As before, electric potential energy of a charge in an electric field is

`U=qV`

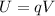
Here we have an electron (charge q=-e) located at point A, where the potential is

`V=k (e)/(2.5)`

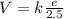
So its electric potential energy this time is

`U=(-e)(k(e)/(2.5))=-k(e^2)/(2.5)`

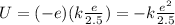
So it's the same as the one calculated at part f), but with a negative sign, since the charge is negative.