For this case we have that by definition, the domain of a function, is given for all the values for which the function is defined.
We have:
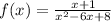
The given function is not defined when the denominator is equal to zero. That is to say:
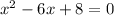
To find the roots we factor, we look for two numbers that when multiplied give as a result "8" and when added as a result "-6". These numbers are:
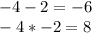
Thus, the factored polynomial is:
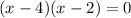
That is to say:
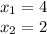
Makes the denominator of the function 0.
Then the domain is given by:
All real numbers, except 2 and 4.
Answer:
x |x≠2,4