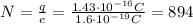Question

Two small spheres spaced 20.0 cm apart have equal charge. How many excess electrons must be present on each sphere if the magnitude of the force of repulsion between them is 4.57 x 10^(-21) N?

Answer 1

894 electrons

Step-by-step explanation:

The electrostatic force between the two charges is given by:

`F=(k q_1 q_2)/(r^2)`

where we have

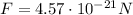`F=4.57\cdot 10^(-21) N` is the force

k is the Coulomb's constant

q1 = q2 =q is the magnitude of the charge on each sphere

r = 20.0 cm = 0.20 m is the distance between the two spheres

Substituting and solving for q, we find the charge on each sphere:

`q=\sqrt{(Fr^2)/(k)}=\sqrt{((4.57\cdot 10^(-21) N)(0.20 m)^2)/(9\cdot 10^9 Nm^2C^(-2))}=1.43\cdot 10^(-16) C`

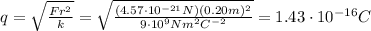
And since each electron has a charge of

`e=1.6\cdot 10^(-19)C`

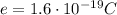
the net charge on each sphere will be given by

`q=Ne`

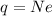
where N is the number of excess electrons; solving for N,

`N=(q)/(e)=(1.43\cdot 10^(-16)C)/(1.6\cdot 10^(-19)C)=894`