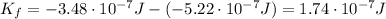Question

In deep space, sphere A of mass 94 kg is located at the origin of an x axis and sphere B of mass 100 kg is located on the axis at x = 1.8 m. Sphere B is released from rest while sphere A is held at the origin. (a) What is the gravitational potential energy of the two-sphere system just as B is released? (b) What is the kinetic energy of B when it has moved 0.60 m toward A?

Answer 1

(a)
`-3.48\cdot 10^(-7) J`

The gravitational potential energy of the two-sphere system is given by

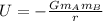`U=-(Gm_A m_B)/(r)` (1)

where

G is the gravitational constant

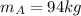`m_A = 94 kg` is the mass of sphere A

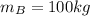`m_B = 100 kg` is the mass of sphere B

r = 1.8 m is the distance between the two spheres

Substitutign data in the formula, we find

`U=-((6.67\cdot 10^(-11))(94 kg)(100 kg))/(1.8 m)=-3.48\cdot 10^(-7) J`

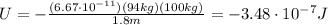
and the sign is negative since gravity is an attractive force.

(b)
`1.74\cdot 10^(-7)J`

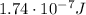
According to the law of conservation of energy, the kinetic energy gained by sphere B will be equal to the change in gravitational potential energy of the system:

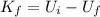`K_f = U_i - U_f` (2)

where

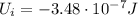`U_i=-3.48\cdot 10^(-7) J` is the initial potential energy

The final potential energy can be found by substituting

r = 1.80 m -0.60 m=1.20 m

inside the equation (1):

U=-\frac{(6.67\cdot 10^{-11})(94 kg)(100 kg)}{1.2 m}=-5.22\cdot 10^{-7} J

So now we can use eq.(2) to find the kinetic energy of sphere B:

`K_f = -3.48\cdot 10^(-7)J-(-5.22\cdot 10^(-7) J)=1.74\cdot 10^(-7)J`