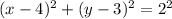Question

Which equation represents the circle described? The radius is 2 units. The center is the same as the center of a circle whose equation is x2 + y2 – 8x – 6y + 24 = 0.

Answer 1

the answer is C

Explanation:

Answer 2

`(x-4)^2+(y-3)^2=2^2`

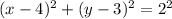
Explanation:

The given circle has equation;
`x^2+y^2-8x-6y+24=0`

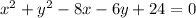
Comparing to the general equation of the circle:
`x^2+y^2+2ax+2by+c=0`

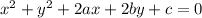
We have
`2a=-8\implies a=-4` and
`2b=-6\implies b=-3`

The center of this circle is (-a,-b)=(4,3).

The required circle has radius r=2 units.

The equation of a circle, given the center (h,k) and radius r, is given by:

`(x-h)^2+(y-k)^2=r^2`

We substitute the values to obtain
`(x-4)^2+(y-3)^2=2^2`