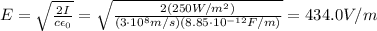Question

A small laser used as a pointer produces a beam of red light 5 mm in diameter, and has a power output of 5 milliwatts. What is the magnitude of the electric field in the laser beam?

Answer 1

434.0 V/m

Step-by-step explanation:

The power output of the laser is:

`P=5 mW = 0.005 W`

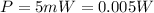
while the radius of the beam is

`r=(5 mm)/(2)=2.5 mm = 0.0025 m`

so the cross-sectional area is

`A=\pi r^2 = \pi (0.0025 m)^2=2.0\cdot 10^(-5) m^2`

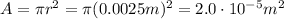
So the intensity of the laser beam is

`I=(P)/(A)=(0.005 W)/(2.0\cdot 10^(-5) m^2)=250 W/m^2`

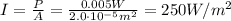
The intensity of a laser beam is related to the magnitude of the electric field by

`I=(1)/(2)c\epsilon_0 E^2`

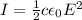
where

c is the speed of light

`\epsilon_0` is the vacuum permittivity

Solving the formula for E, we find

`E=\sqrt{(2I)/(c\epsilon_0)}=\sqrt{(2(250 W/m^2))/((3\cdot 10^8 m/s)(8.85\cdot 10^(-12) F/m))}=434.0 V/m`