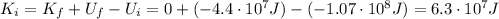Question

Zero, a hypothetical planet, has a mass of 5.3 x 1023 kg, a radius of 3.3 x 106 m, and no atmosphere. A 10 kg space probe is to be launched vertically from its surface. (a) If the probe is launched with an initial kinetic energy of 5.0 x 107 J, what will be its kinetic energy when it is 4.0 x 106 m from the center of Zero? (b) If the probe is to achieve a maximum distance of 8.0 x 106 m from the center of Zero, with what initial kinetic energy must it be launched from the surface of Zero?

Answer 1

(a)
`3.1\cdot 10^7 J`

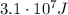
The total mechanical energy of the space probe must be constant, so we can write:

`E_i = E_f\\K_i + U_i = K_f + U_f` (1)

where

`K_i` is the kinetic energy at the surface, when the probe is launched

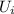`U_i` is the gravitational potential energy at the surface

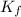`K_f` is the final kinetic energy of the probe

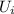`U_i` is the final gravitational potential energy

Here we have

`K_i = 5.0 \cdot 10^7 J`

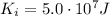
at the surface,
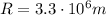`R=3.3\cdot 10^6 m` (radius of the planet),
`M=5.3\cdot 10^(23)kg` (mass of the planet) and m=10 kg (mass of the probe), so the initial gravitational potential energy is

`U_i=-G(mM)/(R)=-(6.67\cdot 10^(-11))((10 kg)(5.3\cdot 10^(23)kg))/(3.3\cdot 10^6 m)=-1.07\cdot 10^8 J`

At the final point, the distance of the probe from the centre of Zero is

`r=4.0\cdot 10^6 m`

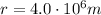
so the final potential energy is

`U_f=-G(mM)/(r)=-(6.67\cdot 10^(-11))((10 kg)(5.3\cdot 10^(23)kg))/(4.0\cdot 10^6 m)=-8.8\cdot 10^7 J`

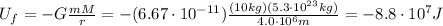
So now we can use eq.(1) to find the final kinetic energy:

`K_f = K_i + U_i - U_f = 5.0\cdot 10^7 J+(-1.07\cdot 10^8 J)-(-8.8\cdot 10^7 J)=3.1\cdot 10^7 J`

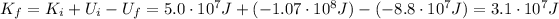
(b)
`6.3\cdot 10^7 J`

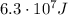
The probe reaches a maximum distance of

`r=8.0\cdot 10^6 m`

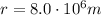
which means that at that point, the kinetic energy is zero: (the probe speed has become zero):

`K_f = 0`

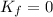
At that point, the gravitational potential energy is

`U_f=-G(mM)/(r)=-(6.67\cdot 10^(-11))((10 kg)(5.3\cdot 10^(23)kg))/(8.0\cdot 10^6 m)=-4.4\cdot 10^7 J`

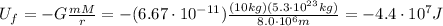
So now we can use eq.(1) to find the initial kinetic energy:

`K_i = K_f + U_f - U_i = 0+(-4.4\cdot 10^7 J)-(-1.07\cdot 10^8 J)=6.3\cdot 10^7 J`