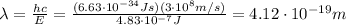Question

(a) Find the energy of the ground state (n = 1) and the first two excited states of an electron in a one-dimensional box of length L = 1.0 10-15 m = 1.00 fm (about the diameter of an atomic nucleus). ground state MeV first excited state MeV second excited state GeV Make an energy-level diagram for the system. (Do this on paper. Your instructor may ask you to turn in this work.) (b) Calculate the wavelength of electromagnetic radiation emitted when the electron makes a transition from n = 2 to n = 1. fm (c) Calculate the wavelength of electromagnetic radiation emitted when the electron makes a transition from n = 3 to n = 2. fm (d) Calculate the wavelength of electromagnetic radiation emitted when the electron makes a transition from n = 3 to n = 1. fm

Answer 1

(a)
`3.77\cdot 10^5 MeV, 1.51\cdot 10^6 MeV, 3.39\cdot 10^3 GeV`

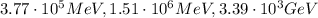
The energy levels of an electron in a box are given by

`E_n = (n^2 h^2)/(8mL^2)`

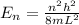
where

n is the energy level

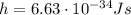`h=6.63\cdot 10^(-34)Js` is the Planck constant

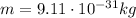`m=9.11\cdot 10^(-31)kg` is the mass of the electron

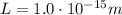`L=1.0\cdot 10^(-15) m` is the size of the box

Substituting n=1, we find the energy of the ground state:

`E_1 = (1^2 (6.63\cdot 10^(-34)^2)/(8(9.11\cdot 10^(-31)(1.0\cdot 10^(-15))^2)=6.03\cdot 10^(-8)J`

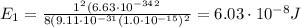
Converting into MeV,

`E_1 = (6.03\cdot 10^(-8) J)/(1.6\cdot 10^(-19) J/eV)\cdot 10^(-6) MeV/eV =3.77\cdot 10^5 MeV`

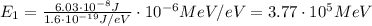
Substituting n=2, we find the energy of the first excited state:

`E_2 = (2^2 (6.63\cdot 10^(-34)^2)/(8(9.11\cdot 10^(-31)(1.0\cdot 10^(-15))^2)=2.41\cdot 10^(-7)J`

Converting into MeV,

`E_2 = (2.41\cdot 10^(-7) J)/(1.6\cdot 10^(-19) J/eV)\cdot 10^(-6) MeV/eV =1.51\cdot 10^6 MeV`

Substituting n=3, we find the energy of the second excited state:

`E_3 = (3^2 (6.63\cdot 10^(-34)^2)/(8(9.11\cdot 10^(-31)(1.0\cdot 10^(-15))^2)=5.43\cdot 10^(-7)J`

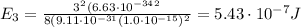
Converting into GeV,

`E_3 = (5.43\cdot 10^(-7) J)/(1.6\cdot 10^(-19) J/eV)\cdot 10^(-9) GeV/eV =3.39\cdot 10^3 GeV`

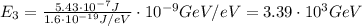
(b)
`1.10 \cdot 10^(-18) m`

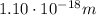
The energy of the emitted radiation is equal to the energy difference between the two levels, so:

`E=E_2 - E_1 = 2.41\cdot 10^(-7)J - 6.03\cdot 10^(-8) J=1.81\cdot 10^(-7) J`

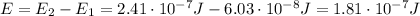
And the energy of the electromagnetic radiation is

`E=(hc)/(\lambda)`

where c is the speed of light; so, re-arranging the formula, we find the wavelength:

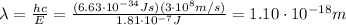
`\lambda=(hc)/(E)=((6.63\cdot 10^(-34) Js)(3\cdot 10^8 m/s))/(1.81\cdot 10^(-7)J)=1.10 \cdot 10^(-18) m`

(c)
`6.59 \cdot 10^(-19) m`

The energy of the emitted radiation is equal to the energy difference between the two levels, so:

`E=E_3 - E_2 = 5.43\cdot 10^(-7) J - 2.41\cdot 10^(-7)J =3.02\cdot 10^(-7) J`

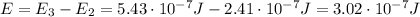
Using the same formula as before, we find the corresponding wavelength:

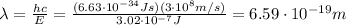
`\lambda=(hc)/(E)=((6.63\cdot 10^(-34) Js)(3\cdot 10^8 m/s))/(3.02\cdot 10^(-7)J)=6.59 \cdot 10^(-19) m`

(d)
`4.12 \cdot 10^(-19) m`

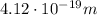
The energy of the emitted radiation is equal to the energy difference between the two levels, so:

`E=E_3 - E_1 = 5.43\cdot 10^(-7) J - 6.03\cdot 10^(-8)J =4.83\cdot 10^(-7) J`

Using the same formula as before, we find:

`\lambda=(hc)/(E)=((6.63\cdot 10^(-34) Js)(3\cdot 10^8 m/s))/(4.83\cdot 10^(-7)J)=4.12 \cdot 10^(-19) m`