Answer:
The same amount of energy is required to either stretch or compress the spring.
Step-by-step explanation:
The amount of energy required to stretch or compress a spring is equal to the elastic potential energy stored by the spring:
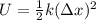
where
k is the spring constant
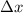 is the stretch/compression of the spring
is the stretch/compression of the spring
In the first case, the spring is stretched from x=0 to x=d, so
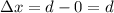
and the amount of energy required is

In the second case, the spring is compressed from x=0 to x=-d, so
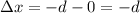
and the amount of energy required is
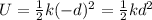
so we see that the amount of energy required is the same.