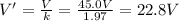(A) 3.9
When a dielectric is inserted between the plates of a capacitor, the capacitance of the capacitor increases according to the equation:
 (1)
(1)
where
C' is the final capacitance
k is the dielectric constant
C is the original capacitance
The capacitance is inversely proportional to the to voltage across the plates:
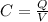 (2a)
(2a)
where Q is the charge stored and V the potential difference across the plates. We can rewrite C' (the capacitance of the capacitor filled with dielectric) as
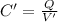 (2b)
(2b)
Substituting (2a) and (2b) into (1), we find
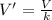 (3)
(3)
where
V = 45.0 V is the original voltage across the capacitor
V' = 11.5 V is the voltage across the capacitor filled with dielectric
Solving for k,
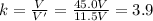
(B) 22.8 V
When the dielectric is partially pulled away, the system can be assimilated to a system of 2 capacitors in parallel, of which one of them is filled with dielectric and the other one is not.
Keeping in mind that the capacitance of a parallel-plate capacitor is proportional to the area of the plates:
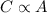
and in this case, the area of the capacitor filled with dielectric is just 1/3 of the total, we can write:
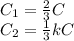
where C1 is the capacitance of the part non-filled with dielectric, and C2 is the capacitance of the part filled with dielectric. The total capacitance of the system in parallel is
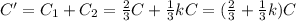
Substituting,
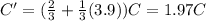
This is equivalent to a capacitor completely filled with a dielectric with dielectric constant k=1.97. Therefore, using again eq.(3), we find the new voltage: