Question

A diverging lens has a focal length of magnitude 22.8 cm. (a) Locate the images for each of the following object distances. 45.6 cm distance 22.8 cm distance 11.4 cm distance

Answer 1

(a) -15.2 cm

We can solve the problem by using the lens equation:

`(1)/(f)=(1)/(p)+(1)/(q)`

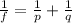
where

f = -22.8 cm is the focal length of the lens (negative because it is a diverging lens)

p = 45.6 cm is the distance of the object from the lens

q is the distance of the image from the lens

Solving the equation for q, we find the position of the image:

`(1)/(q)=(1)/(f)-(1)/(p)=(1)/(-22.8 cm)-(1)/(45.6 cm)=-0.066 cm^(-1)`

`q=(1)/(-0.066 cm^(-1))=-15.2 cm`

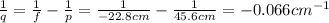
and the negative sign means that the image is virtual.

(b) -11.4 cm

In this case, the distance of the object from the lens is

p = 22.8 cm

Substituting into the lens equation, we can find the new image distance, q:

`(1)/(q)=(1)/(f)-(1)/(p)=(1)/(-22.8 cm)-(1)/(22.8 cm)=-(2)/(22.8 cm)`

`q=(-22.8 cm)/(2)=-11.4 cm`

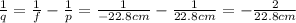
and the negative sign means that the image is virtual.

(c) -7.6 cm

In this case, the distance of the object from the lens is

p = 11.4 cm

Substituting into the lens equation, we can find the new image distance, q:

`(1)/(q)=(1)/(f)-(1)/(p)=(1)/(-22.8 cm)-(1)/(11.4 cm)=-0.132 cm^(-1)`

`q=(1)/(0.132 cm^(-1))=-7.6 cm`

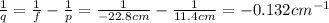
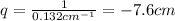
and again, the negative sign means that the image is virtual.