1 Answer

Parthasarathy B · Answer 1 · 2020-11-13T02:23:46+0000

First of all, we compute the points of interest, i.e. the points where the curve cuts the x axis: since the expression is already factored, we have

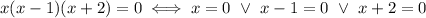
$x(x-1)(x+2) = 0 \iff x=0\ \lor\ x-1=0\ \lor\ x+2=0$

Which means that the roots are

$x=0\ \lor\ x=1\ \lor\ x=-2$

Next, we can expand the function definition:

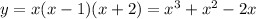
y = x(x-1)(x+2) = x^3 + x^2 - 2x

In this form, it is much easier to compute the derivative:

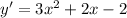
y' = 3x^2+2x-2

If we evaluate the derivative in the points of interest, we have

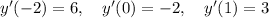
$y'(-2) = 6,\quad y'(0)=-2,\quad y'(1)=3$

This means that we are looking for the equations of three lines, of which we know a point and the slope. The equation

y-y_0=m(x-x_0)

is what we need. The three lines are:

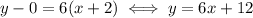$y-0=6(x+2) \iff y = 6x+12$ This is the tangent at x = -2

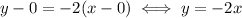$y-0=-2(x-0) \iff y = -2x$ This is the tangent at x = 0

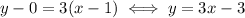$y-0=3(x-1) \iff y = 3x-3$ This is the tangent at x = 1

Please log in or register to add a comment.