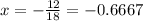Question

9x^2-4=0 find two real solutions

Answer 1

The two real solutions are
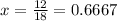`x=(12)/(18) = 0.6667` and
`x=-(12)/(18) =-0.6667`

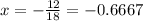
Explanation:

The equation
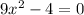`9x^(2) -4=0` is a quadratic function of the form
`ax^(2) +bx+c=0` that can be solved by using the Quadratic Formula.

`x=\frac{-b±\sqrt{b^(2) -4ac} }{2a}`

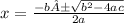
The plus and minus mean that the equation has two solution.

In order to identify is the equation has two real solutions we use the discriminant equation
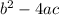`b^(2) -4ac`. Depending of the result we got:

1. If the discriminant is positive, we get two real solutions.

2. if the discriminant is negative, we get complex solutions.

3. If the discriminant is zero, we get just one solution.

Solution:

The equation
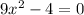`9x^(2) -4=0` has a=9, b=0, and c=-4

Using the discriminant equation to know if the quadratic equation has two real solutions:

`b^(2) -4ac`

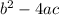
`0^(2) -4(9)(-4)=144` The discriminant is positive which mean we get two real solutions.

Using the Quadratic Formula

`x=\frac{-b±\sqrt{b^(2) -4ac} }{2a}`

`x=\frac{-0±\sqrt{0^(2) -4(9)(-4)} }{2(9)}`

`x=(±√(144) )/(18)`

`x=±(12)/(18)`

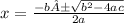
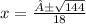
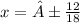
then

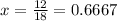`x=(12)/(18) = 0.6667` and
`x=-(12)/(18) =-0.6667`