Answer:
The rate of decay each month is -0.006924%
Explanation:
The cost of a car after 1 year at a 8% decreased
Decreased price = Sale price - (Sale price x porcentage of decreased/100%)
Decreased price = $20,000 - ($20,000 x 8%/100%)
Decreased price = $20,000 - ($20,000 x 0.08)
Decreased price = $20,000 - $1,600 = $18,400
So, the value of the car decreased by 8% in a year is $18,400.
The general equation for exponential decay is:
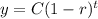
Where
y = final amount
C = Sale price
r = rate of decay
t = time
We know that the sale price was $20,000. After a year the decreased price is $18,400.
From the general equation for exponential decay, our sale price is $20,000 decreased over a time of 12 months resulting the final amount of $18,400.
substituting the values
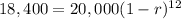
Solving the equation for r
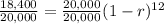
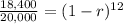
![(18,400)/(20,000)^{(1)/(12) } =[(1-r)^(12)]^{(1)/(12)}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/p6u3hwbc16v7t33ccw3kelr1pfqxmp9d28.png)
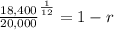
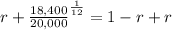
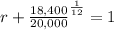
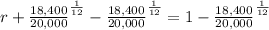

![r=1-\sqrt[12]{(18,400)/(20,000)}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/n2ip7h994hrno3mcq35r586gupdxuzk5rx.png)
![r=1-\sqrt[12]{0.92}\\r=1-0.993076\\r= -0.006924](https://img.qammunity.org/2020/formulas/mathematics/middle-school/w3pfufymaxy82gt11xudtr115rlnemaoan.png)