Answer:
The minimum number of rolls to buy is 9
Explanation:
step 1
Find the perimeter of the ceiling of Katie’s living room
The perimeter of a square is equal to
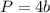
where
b is the length side of the square
we have
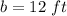
so
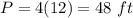
step 2
Find the length side of the diagonals of the ceiling
Applying Pythagoras theorem
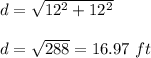
step 3
Find the total crepe paper needed
Sum the perimeter plus two times the length side of the diagonal
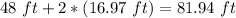
step 4
Find the number of rolls needed
we know that
Each roll contain 10 ft of crepe paper
so

Round up

The minimum number of rolls to buy is 9