Question

A merchant wants to blend 80 pounds of cacao worth $9.00 a pound from two kinds: one at $11.40 a pound and the other at $7.80 a pound. How many pounds of each kind should he mix?

Answer 1

he should mix 16lbs of the 7.80 mix and 8lbs of the 11.40 mix

Explanation:

hope this helps:) btw im a student at rsm and i got this for homework so ya. your welcome also, ik the answers wrong ...s i g h...

Answer 2

The merchant should mix 53.33 pounds of cheaper cacao and 26.67 pounds of costlier cacao.

Explanation:

A merchant wants to blend 80 pounds of cacao worth $9.00 a pound from two kinds: one at $11.40 a pound and the other at $7.80 a pound.

Let the number of pounds of cheaper cacao be x

Let the number of pounds of costlier cacao be y

The merchant wants total pounds = 80

So, first equation becomes:

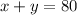`x+y=80` or
`x=80-y`

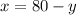
Now values of per pounds become
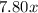`7.80x` and
`11.40y`

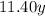
As the merchant wants the mixture worth $9 so second equation becomes:

`7.80x+11.40y=9(80)`

=>
`7.80x+11.40y=720`

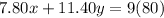
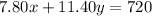
Substituting
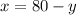`x=80-y` in second equation, we get

`7.80(80-y)+11.40y=720`

=>
`624-7.80y+11.40y=720`

=>
`3.60y=96`

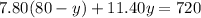
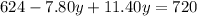
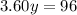
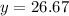`y=26.67` pounds

We know,
`x=80-y`

=>
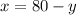
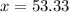`x=53.33` pounds

So, The merchant should mix 53.33 pounds of cheaper cacao and 26.67 pounds of costlier cacao.

We can check this:

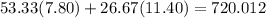`53.33(7.80)+26.67(11.40)=720.012` dollars