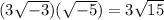Answer:
The product is equal to

Explanation:
Ok,
First, you have
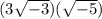
We must follow the rule for multiplying radicals, in this case:
![(3\sqrt[2]{-3})(\sqrt[2]{-5})=(3\sqrt[2]{(-3)(-5)})](https://img.qammunity.org/2020/formulas/mathematics/high-school/iq6upcjjd2adlrdd5wpnd6f8xg9gnxzmx2.png)
Note that the types of root, n, have to match, in this case is 2 for each root
Then, we know that two negative numbers multiplied give a positive number, in this case
![(3\sqrt[2]{-3} )(\sqrt[2]{-5})=(3\sqrt[2]{(-3)(-5)})=(3\sqrt[2]{(15)})](https://img.qammunity.org/2020/formulas/mathematics/high-school/h7i3hyfl0ws3ws64sq4yjp0f1qfvdi2c2n.png)
So, the correct answer is