Question

(25pts) Due soon! Help!

Answer 1

true

True

False

False

Explanation:

Answer 2

true

True

False

False

Explanation:

a. The problem tells me that for every 3 parts of red paint, I have 8 parts of yellow paint. To find the ratio of 1 part of yellow paint I can write the following statement

For 8 parts of yellow paint ------------ 3 parts of red paint

1 part of yellow paint ------------- x

So
`x=(1 part of yellow paint * 3 parts of red paint )/(8 parts of yellow paint)`

`x= (3)/(8) parts of red paint`

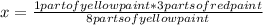
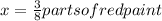
b, I have the following relationship

3 parts of red paint ----- 8 parts of yellow paint

If I multiply the entire expression by 3 I have left

3 * 3 parts of red paint -------- 8 * 3 parts of yellow paint

So

9 parts of red paint ---------- 24 parts of yellow paint

c.I have the same relationship

3 parts of red paint ----- 8 parts of yellow paint

If I multiply the entire expression by 1/2 I have left

3/2 parts of red paint -------- 8/2 parts of yellow paint

So

3/2 parts of red paint ---------- 4 parts of yellow paint

as 3/2 is different from 10, then the approach is false

d. observing the relation of part a,

For 3 parts of red paint ------------ 8 parts of yellow paint

1 part of red paint ------------- x

So
`x=(1 part of red paint * 8 parts of yellow paint )/(3 parts of red paint)`

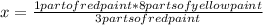
`x= (8)/(3) parts of yellow paint` that is different than 3/8 parts of yellow paint, then the approach is false