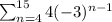Question

Given the sequence in the table below, determine the sigma notation of the sum for term 4 through term 15.

n an
1 4
2 −12
3 36

Answer 1

`\bf \begin{array}ll \cline{1-2} n&a_n\\ \cline{1-2} 1&4\\ &\\ 2&\stackrel{4(-3)}{-12}\\ &\\ 3&\stackrel{-12(-3)}{36}\\ \cline{1-2} \end{array}\qquad \impliedby \textit{common ratio of`

`\bf \qquad \qquad \textit{sum of a finite geometric sequence} \\\\ S_n=\sum\limits_(i=1)^(n)\ a_1\cdot r^(i-1)\implies S_n=a_1\left( \cfrac{1-r^n}{1-r} \right)\quad \begin{cases} n=n^(th)\ term\\ a_1=\textit{first term's value}\\ r=\textit{common ratio}\\[-0.5em] \hrulefill\\ r=-3\\ a_1=4\\ n=15 \end{cases} \\\\\\ S_(15)\implies \displaystyle\sum\limits_(i=4)^(15)~4(-3)^(i-1)`

Answer 2

`\sum_(n=4)^(15)4(-3)^(n-1)`

Explanation:

The given sequence is 4, -12, 36

We can see there is a common ratio

`(a_(2) )/(a_(1) )` =
`(-12)/(4)=(-3)`

`(a_(2) )/(a_(3) )` =
`(36)/(-12)=(-3)`

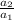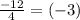
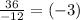
Therefore, the given sequence is a geometric sequence.

Now we have to determine the sigma notation of the sum for term 4 through term 15.

Since explicit formula of the sigma can be represented as

`T_(n)=a(r)^(n-1)`

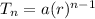
where
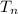`T_(n)` = nth term

a = first term

n = number of term term

r = common ratio

and sum is denoted by
`\sum_(n=1)^(n)a(r)^(n-1)`

Now for the given sequence sigma notation will be

`\sum_(n=4)^(15)4(-3)^(n-1)`