Question

Find an explicit rule for the nth term of a geometric sequence where the second and fifth terms are -6 and 162, respectively.

Select one:
a. an = 2 • 3n - 1
b. an = 2 • (-3)n - 1
c. an = 2 • 3n
d. an = 2 • (-3)n + 1

Answer 1

b. an = 2 • (-3)^(n - 1)

Explanation:

Before we test a solution or two, we can easily discard most of them.

We see the values alternate of signs (-5 for the 2nd term and +162 for the 5th term)... so the progression factor has to be negative (in order to alternate sign). That already excludes answers A and C.

Normally, a geometric progression has the (n-1) exponent, not (n+1), so our chances seem to be better with B.

We can test both D and B with n = 2, to obtain -6

Let's test answer D before:

`a_(2) = 2 * (-3)^(2+1) =  2 * (-3)^(3) = 2 * -27 = -54`

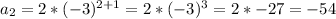
The result is -54, not -6... so it's not the right result.

Let's test answer B then:

`a_(2) = 2 * (-3)^(2-1) =  2 * (-3)^(1) = 2 * -3 = -6`

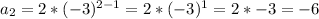
Right! Let's verify with n=5 to get 162:

`a_(5) = 2 * (-3)^(5-1) =  2 * (-3)^(4) = 2 * 81 = 162`

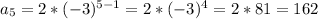
Confirmed, answer is B. an = 2 • (-3)^(n - 1)