Question

Which of the following is a polynomial function in standard form with zeros at -8,-1 and 3? Help needed!!! 10 points!!! Math 3

Answer 1

`f(x) = {x}^(3) + 6 {x}^(2) - 19 - 24`

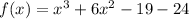
Step-by-step explanation

The polynomial function has zeros at:

-8,-1 and 3

This means the polynomial can be factored as:

`f(x) = (x + 8)(x + 1)(x - 3)`

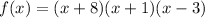
We expand the last two factors:

`f(x) = (x + 8)( {x}^(2) - 2x - 3)`

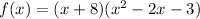
We expand further to get:

`f(x) = {x}^(3) - 2 {x}^(2) - 3x + 8 {x}^(2) - 16x - 24`

`f(x) = {x}^(3) + 6 {x}^(2) - 19 - 24`

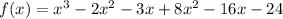
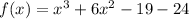
The polynomial in descending powers of x is said to be in standard form.