Answer:
Nothing
Step-by-step explanation:
The radius of the orbit of the Earth does not depend on the radius of the sun.
In fact, the gravitational attraction between the Earth and the Sun provides the centripetal force that keeps the Earth in orbit:
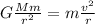
where
G is the gravitational constant
M is the mass of the sun
m is the mass of the Earth
r is the radius of the orbit of the Earth
v is the orbital speed of the earth
Re-arranging the equation for r:

Also,
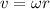
where
 is the angular velocity of the Earth's orbit. So we can rewrite the equation as
is the angular velocity of the Earth's orbit. So we can rewrite the equation as
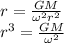
As we see, the radius of the orbit of the Earth, r, does not depend on the mass of the Sun, so if the sun shrank in size, the orbit remains the same.