Answer:
1. C, (-1,0) and (5,0)
2. B, a = -2, b = 6, c = 2
Explanation:
1. the x-intercepts can be determined as where the parabola crosses the x-axis, in this case it crosses twice. your answer is correct that the x-intercepts are (-1,0) and (5,0)
2. to solve y = 3x² - 12x - 36 we are told that the x terms for a & b (3x² and -12x respectively) are 0, where a < b. to solve this, we factor the equation
3x² - 12x - 36 has a GCF of 3, so we can factor our a 3
3(x² - 4x - 12)
now we can factor out x² - 4x - 12. to factor we need 2 numbers that when multiplied together give us -12 and when added together give us -4. our answer to this is -6 and 2
3(x - 6)(x + 2)
we now use the zero product property rule by setting each expression = to 0 and solve
x - 6 = 0 < add 6 to both sides
x = 6
x + 2 = 0 < subtract 2 from both sides
x = -2
we know that a and b are 0s and that a < b. we now know that a = -2 and b = 6
to find c, we need to find the x-coordinate as we are given a minimum point. to do this, we use the formula c =
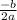using the b and a terms from the ORIGINAL EQUATION
a = 3 and b = -12
c =
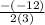
c =
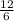
c = 2
our c term is 2
with these terms in mind, we see that a = -2, b = 6, and c = 2. the only answer that matches this is B, which is our answer.